![]()
![]()
|
|
2. De fysieke principes van het vliegen1)2.1 InleidingZowel tijdens het opstijgen, als tijdens de vlucht en het landen van een vliegtuig werken er een heleboel krachten op in. Deze krachten worden onder andere veroorzaakt door het vleugeloppervlak, de snelheid van het vliegtuig, de wind, het gewicht. In dit hoofdstuk bespreken wij deze krachten, die zowel gelden voor de C-130H Hercules als voor elk ander type vliegtuig. In onze figuren en grafieken gebruiken we meestal de Cessna als model om de fysieke principes van het vliegen uit te leggen. 2.2 De hoofdkrachtenBij de aŽrodynamische krachten die tijdens een vlucht op een vliegtuig werken, zijn er vier basiskrachten. Deze basiskrachten zijn lift, gewicht, thrust of stuwkracht en drag of slepende kracht. Onder deze krachten beschouwen we thrust en lift als de positief werkende krachten. Gewicht en drag zijn dan de negatief werkende krachten. Hier bespreken we deze vier hoofdkrachten.
2.2.1 De lift2)Lift is de opwaartse kracht gerealiseerd door een draagvlak wanneer dit door de lucht beweegt. Aan een vliegtuig zijn er drie draagvlakken: de vleugels, de propeller en het horizontale staartoppervlak. Door het principe van Bernoulli en een wet van Newton kunnen we begrijpen hoe lift wordt geproduceerd. Het principe van Bernoulli zegt: "De inwendige druk van een stroming (vloeistof of gas) stijgt op het punt waar de snelheid van de stroming daalt." Formule:
We bouwen deze formule om:
Het hoogteverschil is verwaarloosbaar tegenover de andere componenten. Nu kan door verschillende factoren, zoals vleugelprofiel, kleppen, rolroeren, e.d., de snelheid van de lucht boven het draagvlak opgedreven worden, zodat de druk boven het draagvlak kleiner wordt t.o.v. de druk onder het draagvlak. Hieruit volgt dat het draagvlak naar boven zal gedrukt worden, of met andere woorden we bekomen lift door de snelheid van de lucht te verhogen boven het draagvlak. Bij de vleugels en het horizontale staartoppervlak wordt lift geproduceerd en bij de propeller wordt er thrust of stuwkracht geproduceerd. Hierdoor kunnen we ook verklaren hoe de drie bewegingen van een vliegtuig ontstaan. Deze drie hoofdbewegingen zijn rollen, stampen en gieren. 2.2.1.1 RollenAls we door het zwaartepunt van het vliegtuig een lijn trekken, van de voorzijde tot de achterzijde van het vliegtuig, dan is rollen de beweging rond deze as.
Als we de linkerrolroeren naar beneden drukken, dan stijgt de snelheid boven het draagvlak en daalt die onder het draagvlak. Nu zal door het principe van Bernoulli de linkervleugel naar boven gedrukt worden. Het omgekeerde gebeurt bij de rechtervleugel, zodat het vliegtuig naar rechts rolt of draait. Het rollen naar links volgt dezelfde redenering. Hier wordt de linkervleugel naar beneden gedrukt en de rechtervleugel naar boven. Bij de linkervleugel is nu het rolroer naar beneden gedrukt en bij de rechtervleugel naar boven. 2.2.1.2 StampenAls we nu een lijn trekken door het zwaartepunt en in de richting van de vleugels, dan is stampen de beweging rond deze lijn.
We gebruiken het horizontale staartoppervlak om te stampen. De neus moet naar beneden gedrukt worden, dus moeten we het staartoppervlak naar boven drukken. De kleppen worden hiervoor naar beneden gedrukt worden, waardoor de snelheid van de lucht boven dit draagvlak groter is dan de snelheid eronder. Weer door het principe van Bernoulli zal een grotere druk naar boven ontstaan dan naar onderen en zo wordt de staart naar boven en de neus naar beneden gedrukt. Het vliegtuig zal dus dalen. Om het vliegtuig te laten stijgen, moeten we het staartoppervlak doen dalen en dus de kleppen van het staartoppervlak naar boven drukken. Dit gebeurt weer via Bernoulli. 2.2.1.3 GierenAls we nu een lijn trekken door het zwaartepunt van het vliegtuig, van beneden naar boven, dan is gieren de beweging rond deze as.
Om deze beweging te veroorzaken, gebruiken we het Ďrudderí of het roer aan de achterzijde van het vliegtuig, dat vertikaal staat. Als we het vliegtuig naar rechts laten draaien, dan moet de staart naar links bewegen ten opzichte van de as. Om de staart naar links te draaien, moeten we het roer naar rechts positioneren, om dan weer vanuit het principe van Bernouilli af te leiden dat de staart inderdaad naar links beweegt. De snelheid van de lucht links van het roer is groter dan aan de rechtse kant. Daardoor is de druk aan de linkerkant groter dan die aan de rechterkant. Hierdoor draait het vliegtuig naar rechts. Merk wel op dat het roer niet kan gebruikt worden om het vliegtuig te laten draaien in de lucht, maar wel om het gieren tegen te gaan of als het vliegtuig beweegt op de grond, bijvoorbeeld bij het op weg zijn naar de startbaan. Bij andere vliegtuigen gebruiken we het neuswiel, zoals bij de C-130H Hercules. De derde wet van Newton luidt: "Voor iedere actiekracht is er een reactiekracht." Een bijkomende opwaartse kracht wordt ontwikkeld als het onderste draagvlak de lucht doet afwijken naar onderen. Dus zowel de ontwikkeling van lage druk als de reactie van de kracht en richting van de lucht die afwijkt van het onderste draagvlak van de vleugel dragen bij tot het genereren van lift. Met andere woorden : de lucht die door een draagvlak naar onderen afgebogen wordt, resulteert in een bijkomende kracht van lift ; dit komt door de wet van actie en reactie.
De hoeveelheid van lift veroorzaakt door de vleugel hangt af van verschillende factoren : de snelheid van de vleugel door de lucht, de invalshoek, de vorm van de vleugel van bovenaf gezien (figuur 5 voor de C-130H), de vleugeloppervlakte en de dichtheid van de lucht. Formule:
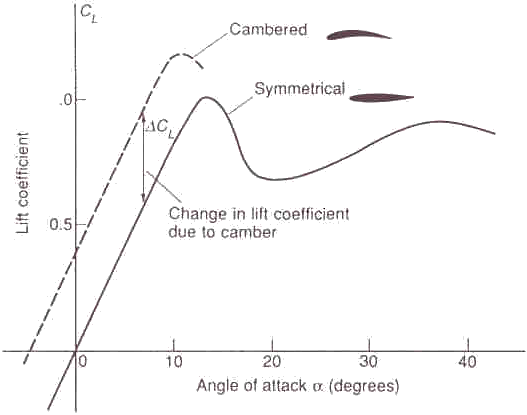
Figuur 6: liftcoŽfficiŽnt in functie van de invalshoek De liftcoŽfficiŽnt van een draagvlak hangt af van de vorm en de invalshoek van dat draagvlak. (zie figuren 6 en 7) Voor de C130H geldt de volle curve, dus een symmetrisch draagvlak.De invalshoek wordt weergegeven in figuur 7. De invalshoek is altijd gebaseerd op de vliegroute en niet op de horizon of de grond. De invalshoek is de hoek tussen de Ďchord lineí en de vliegroute. 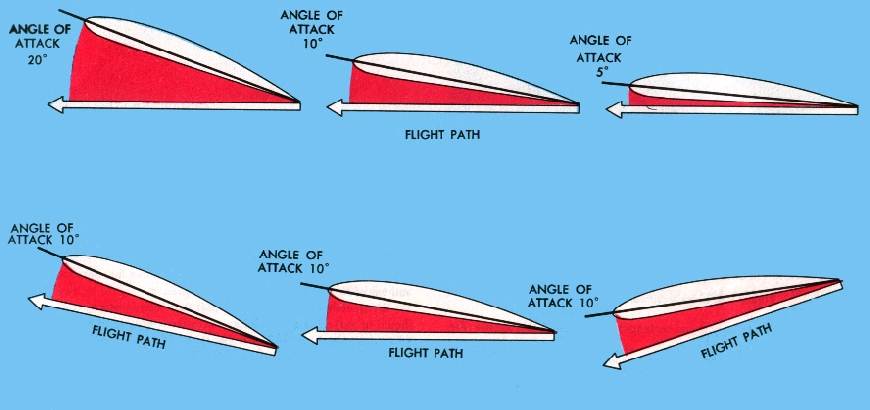 Figuur 7: verschillende invalshoeken
2.2.2 De 'thrust' of stuwkrachtDit is de kracht die de motor veroorzaakt. Bij de C130H hebben we vier stuwkrachten. Deze vier krachten moeten we herleiden tot ťťn kracht die door het zwaartepunt van het vliegtuig loopt. ĎThrustí is de voorwaartse kracht door het zwaartepunt.
We berekenen deze stuwkracht voor ťťn motor. Dit draaimoment delen we door 4,56 inch-pounds, dit omdat 1 pk overeenkomt met 4,56 inch-pounds van het draaimoment. 1 pk komt overeen met een vermogen van 736 Watt. De snelheid van het vliegtuig kan de piloot ook aflezen in de cockpit, maar hij leest die snelheid af in knopen. De snelheid moet in meter per seconde uitgedrukt worden. 1 knoop komt overeen met 0,5144 meter per seconde. We schrijven deze formule als volgt:
Voor het vermogen :
Voor de snelheid:
Voor de trekkracht:
Dit is de trekkracht gerealiseerd voor ťťn motor. Voor de vier motoren samen moeten we de trekkracht gerealiseerd door elke motor afzonderlijk, samenstellen tot ťťn trekkracht door het zwaartepunt. Dit is het samenstellen van 4 evenwijdige coplanaire krachten. Nu is de totale gerealiseerde kracht van de vier motoren samen door het zwaartepunt gelijk aan 4xF. 2.2.3 Het gewichtHet gewicht is de kracht die veroorzaakt wordt door het vliegtuig en de lading. Gewicht wordt gelijkgesteld aan de gravitatiekracht en is eenvoudig te berekenen. Met:
Deze kracht grijpt net als thrust en lift aan in het zwaartepunt. Gewicht werkt altijd naar het middelpunt van de aarde toe. 2.2.4 De drag of slepende kracht3)Drag is de kracht die naar achter toe werkt en tegengesteld is aan de beweging van het vliegtuig door de lucht. Drag werkt parallel aan de windrichting. Elk deel van het vliegtuig dat blootgesteld wordt aan de lucht, terwijl het vliegtuig in beweging is, produceert weerstand en draagt bij tot de totale drag. De totale drag wordt onderverdeeld in geÔnduceerde drag en parasiete drag. 2.2.4.1 De geÔnduceerde dragDit is de ongewenste, maar onvermijdelijke drag die voortkomt uit de lift en daalt als de invalshoek vermindert. Dus hoe groter de invalshoek, hoe groter de lift en hoe groter de drag. M.a.w. hoe groter de invalshoek, hoe meer weerstand het vliegtuig ondervindt tijdens de voorwaartse beweging. Formule:
De dragcoŽfficiŽnt hangt af van de invalshoek, dus ook van de lift, het ĎReynolds- numberí en het ĎMach numberí.
Als de invalshoek gekend is, kunnen we de dragcoŽfficiŽnt terugvinden in grafieken zoals in figuur 10. Deze invalshoek is identiek als die bij de lift. Het Reynolds-nummer Deze invloedsfactor is laag in het wijdse luchtruim en bij berekeningen voor vliegtuigen wordt dan ook geen rekening gehouden met het Reynolds-nummer. De formule van het Reynolds-nummer:
Deze formule werken we uit voor een staafje dat in een luchtstroom beweegt. Via een grafiek kunnen we uit dit RN de dragcoŽfficiŽnt halen (figuur 11).
Het mach-number Hiermee wordt ook geen rekening gehouden voor vliegtuigen waarvan de snelheid lager ligt dan de helft van de geluidssnelheid (=331 m/s). Het ĎMach-numberí is de snelheid van het vliegtuig gedeeld door de geluidssnelheid. In de praktijk zullen we alleen rekening houden met de invalshoek om de drag te berekenen. 2.2.4.2 De parasiete dragDit is de drag veroorzaakt door ieder vliegtuigdeel dat geen lift veroorzaakt. Verschillende factoren beÔnvloeden deze parasiete drag. Deze factoren zijn : dichtheid van de lucht, de vorm, de grootte en de snelheid van het object. Parasiete drag kunnen we verder onderverdelen in gevormde drag, wrijving, en interferente drag. De gevormde drag Dit is de drag gevormd door vliegtuigonderdelen die frontaal staan ten opzichte van de luchtstroom. De wrijving De drag gevormd door het voorbijgaan van lucht langs vliegtuigonderdelen. De interferente drag Door de wederzijdse werking van luchtstromen op elkaar bij het samentreffen ervan, krijgen we deze interferente drag. 2.2.4.3 De totale dragDoor de geÔnduceerde en de parasiete drag samen te tellen, krijgen we de totale drag. Als de geÔnduceerde drag groter is dan de parasiete drag, dan hebben we een Ďstallí, of verliezen we vliegsnelheid (figuur 12). 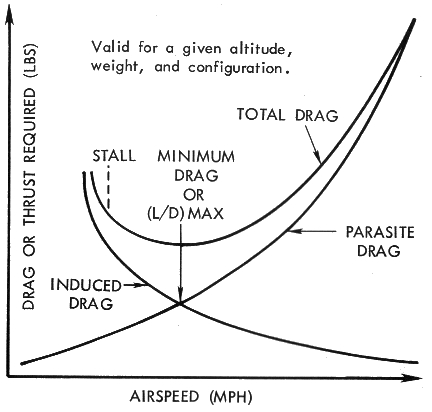 Figuur 12: drag in functie van de vliegsnelheid 2.2.5 BesluitDe krachten die inwerken op het vliegtuig worden vooral veroorzaakt door de invalshoek, de dichtheid van de lucht, de snelheid, de motor, de druk, de vleugeloppervlakte en het gewicht. 2.3 Inwerkende krachten op een vliegtuig tijdens een klim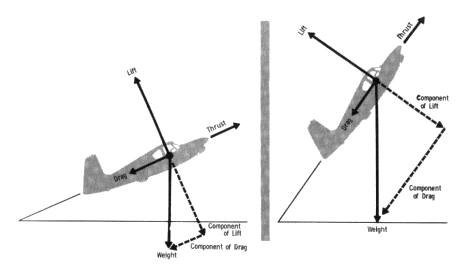 Figuur 13: inwerkende krachten tijdens een klim Als we het toestel onder een hoek brengen, waardoor de neus van het toestel naar boven gericht is, dan zien we dat er twee bijkomende krachten ontstaan. Er komen twee componenten bij: een componente van lift en een componente van drag. Als we de krachten, lift, thrust en drag optellen en als deze resultante gelijk is aan het gewicht, dan is het toestel in evenwicht. Voor deze zes krachten die nu op ons toestel inwerken tijdens een klim gelden volgende formules: 2.3.1 De thrustVoor de thrust, of stuwkracht blijft de formule gelijk, zoals beschreven in 2.2.2:
2.3.2 De liftHier blijft de formule dezelfde zoals beschreven bij 2.2.1:
2.3.3 De dragHier geldt ook dezelfde formule als in onderdeel 2.2.4: Met:
2.2.4 Het gewichtOok hier geldt dezelfde formule : G = m . g
2.3.5. De componente van dragDeze werkt in dezelfde zin en richting als de hoofdkracht drag. Cd = m . g . cos q
2.3.6 De componente van liftDeze werkt in tegengestelde zin en in dezelfde richting als de hoofdkracht lift. Cd = m . g . sin q
2.3.7 OpmerkingDe hoek q , gebruikt in de twee laatste formules, is de klimhoek. Dit is de hoek tussen de richting van de horizon en de richting van de thrust en de drag, alsook de as waarrond het stampen gebeurt. Deze hoek kunnen we aflezen in de cockpit op de kunstmatige horizon. Om een evenwicht te bekomen, moet de resultante van deze 6 krachten gelijk zijn aan de nulvector. 2.4 Inwerkende krachten op een vliegtuig tijdens een daling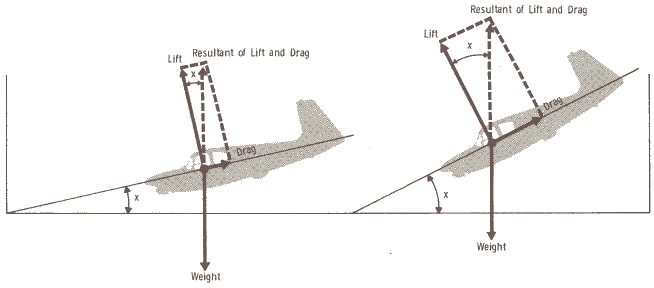 Figuur 14: inwerkende krachten tijdens een daling Door het hellen van het vliegtuig vormt zich nu een resultante van lift en drag. Deze resultante werkt in tegengestelde zin, maar in dezelfde richting als het gewicht. We krijgen weer de formules voor de vier hoofdkrachten (zie bij 2.3). Daarnaast komt de formule voor de resultante van lift en drag. Formule :
2.5 Inwerkende krachten op een vliegtuig tijdens een bocht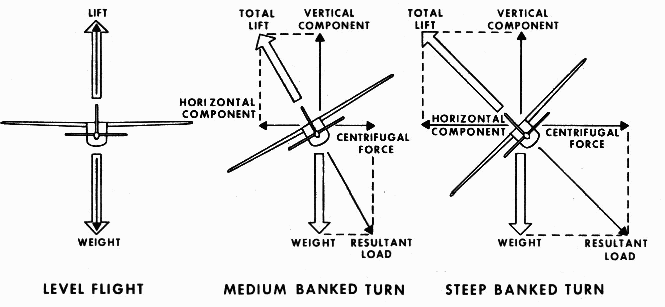 Figuur 15: inwerkende krachten tijdens een bocht 2.5.1 Waarom draait een vliegtuig?Om het vliegtuig te laten draaien, gebruiken we de gewone lift van het vliegtuig. Die lift staat altijd loodrecht op het vleugeloppervlak (figuur 15). We krijgen dus een horizontale componente van lift, naar de binnenkant van de bocht toe. We gebruiken de derde wet van Newton, die zegt dat er voor iedere kracht een reactiekracht is, en zien we dat er een centrifugale kracht ontstaat. De rest van de krachten zoals gewicht, thrust en drag blijven. Anders gezegd, het draaien van het vliegtuig gebeurt door de liftcomponente op te delen in een vertikale en een horizontale componente, waardoor er ook een centrifugale kracht ontstaat. 2.5.2 Krachten die inwerken op een vliegtuig tijdens een bochtWe hebben nu volgende 8 krachten : lift, een horizontale componente van lift, een vertikale componente van lift, een centrifugale kracht, gewicht, resultante van het gewicht, drag en thrust. Formules: 2.5.2.1 De liftHier blijft de formule dezelfde zoals beschreven in 2.2.1: Met:
2.5.2.2 De horizontale componente van liftWe kunnen de hoek, die een vliegtuig maakt t.o.v. de horizon aflezen in de cockpit op de kunstmatige horizon. Dit is niet dezelfde hoek die we hadden bij de bespreking van de krachten bij een klim of daling van een vliegtuig. Volgende formule is nu van toepassing:
2.5.2.3 De vertikale componente van liftMet:
2.5.2.4 De centrifugale krachtDie is gelijk in grootte, maar tegengesteld van zin aan de horizontale componente van lift. Dus hier geldt dezelfde formule als in 2.5.2.2. 2.5.2.5 Het gewichtHier geldt weer dezelfde formule: G = m . g
2.5.2.6 De resultante van het gewichtMet:
2.5.2.7 De dragMet:
2.5.2.8 De thrustMet:
2.5.2.9 OpmerkingOm een evenwicht te bekomen, moet de resultante van deze acht krachten gelijk zijn aan de nulvector. 2.6 BesluitWe plaatsen de verschillende situaties nog even op een rij. 2.6.1 Krachten tijdens een gewone horizontale vlucht, zonder dalen of klimmenHier hadden we de volgende vier krachten:
Deze krachten zijn de vier hoofdkrachten van het vliegtuig. Bij lift bespraken we dan de drie hoofdbewegingen van een vliegtuig: rollen, stampen en gieren. 2.6.2 Krachten tijdens een klimHierbij hadden we de volgende zes krachten:
Hierbij gelden, voor de vier hoofdkrachten, weer dezelfde formules. Aangezien we het toestel laten hellen, wordt het gewicht, dat altijd naar de aarde gericht is, opgedeeld in een componente van drag, positief werkend op de hoofddrag en een componente van lift, negatief werkend op de hoofdlift. 2.6.3 Krachten tijdens een dalingHierbij zijn volgende krachten aanwezig:
2.6.4 Krachten tijdens een bochtHierbij zijn de volgende acht krachten aanwezig:
Bij een bocht wordt lift verdeeld in twee componenten, waardoor ook een centrifugale kracht ontstaat. Als we al deze situaties bekijken, kunnen we zeggen dat er vier hoofdkrachten, lift, thrust, drag en gewicht zijn, die bij iedere beweging opgesplitst worden in verschillende componenten. 1) Pilot Ďs Handbook of Aeronautical Knowledge, U.S. Department
of Transportation, Federal Administration, Washington D.C., 1984, p 1 - 31
|
|
Teken
mijn gastenboek Laaste wijziging maandag 13 maart 2000
|